2022. 2. 24. 12:01ㆍData Analysis/Machine Learning

안녕하세요.
데이터 분석하는 랩장 대학원생, 석사 3학기 고니입니다.
이번 시간에는 의사결정나무에 대해 이야기를 나누어보려고 합니다. 본격적으로 머신러닝 모형에 대해 다루는 첫 번째 포스팅이 되겠습니다! 지난 포스팅에서는 클래스 불균형 자료와 샘플링 기법에 대해 이야기를 나누었는데 기억나시나요? 클래스 불균형과 샘플링이라는 두 개념 모두 범주형 변수를 타겟변수로 가지는 분류모형을 대상으로 하는 것들이었습니다. 혹시 기억이 잘 나지 않으신다면 지난 포스팅을 참고해주세요!
의사결정나무는 가장 대표적인 분류모형 중 하나입니다. 물론 연속형 타겟변수를 가지는 예측 문제에 대해서도 사용할 수는 있으나 일반적으로는 분류 문제에 주로 사용하곤 합니다. 정말 단순한 알고리즘을 가지고 있으면서도 높은 성능과 결과 해석의 간편함을 자랑하여 많은 사랑을 받고 있는 모형입니다. 저도 데이터 분석을 할 때마다 의사결정나무는 꼭 한 번씩 사용하는 것 같습니다.
자, 그러면 의사결정나무에 대해 함께 자세히 살펴볼까요?
# 의사결정나무(Decision Tree)
차근차근 시작해봅시다. 우선 의사결정나무라는 이름부터 해석해봅시다. 의사결정나무를 한 단어씩 뜯어보면 '의사', '결정', '나무'가 됩니다. 세 가지 단어의 사전적 정의를 살펴보면 아래의 사진과 같습니다.



즉, 의사결정나무는 생각을 정해주는 나무를 의미합니다. 판단을 내려주는 나무라고 생각하시면 좋을 것 같습니다. 잠시 후에 그림으로 보여드리겠지만 생긴 것도 정말 나무처럼 생겼습니다. 우리가 의사결정나무에 데이터를 넣어주면 의사결정나무는 어떠한 규칙에 의해 정답이 무엇인지를 판단하여 우리에게 알려줍니다. 예를 들어 메일 데이터를 넣어주면 의사결정나무는 어떠한 규칙에 의해 해당 메일이 스팸 메일인지 아닌지를 스스로 판단하여 우리에게 알려줄 수 있습니다. 어떠한 규칙이라는 것이 무엇인지에 대해서는 잠시 후에 자세히 다루도록 하겠습니다!
의사결정나무는 크게 두 가지로 나눌 수 있는데, 위의 스팸 메일 분류 예시처럼 범주형 타겟변수에 대해 분류를 수행하는 의사결정나무를 분류나무라고 하고, 주가 예측과 같이 연속형 타겟변수에 대해 예측을 수행하는 의사결정나무를 회귀나무라고 부릅니다.
정리하면 의사결정나무는
"데이터를 분석하여 그들 사이의 패턴과 결과를 나무 구조로 모형화하여 나타내는 분류 및 예측 모형"
이라고 할 수 있습니다. 갑자기 설명이 확 어려워져서 어떤 말인지 이해가 잘 되지 않으신다고요? 지금부터 저와 함께 하나씩 살펴보시면 쉽게 이해가 되실겁니다!
# 의사결정나무의 구조
위에서 의사결정나무는 생긴 것도 정말 나무처럼 생겼다고 말씀드렸습니다. 그림을 통해 구조를 살펴보시면 확 와닿으실겁니다. 실제로 의사결정나무를 구성하고 있는 각 부분들의 명칭도 뿌리, 가지, 잎과 같이 실제 나무를 구성하고 있는 부분들의 명칭과 동일합니다. 함께 그림을 살펴보시죠!

왼쪽의 그림이 의사결정나무이고, 오른쪽의 그림은 우리가 알고 있는 나무입니다. 정말 비슷하게 생기지 않았나요? 의사결정나무는 우리가 알고 있는 나무를 거꾸로 뒤집어 놓은 형태입니다. 맨 위에 있는 부분을 뿌리마디라고 부르고, 중간에 있는 부분들을 중간마디, 그리고 더이상 갈라지지 않고 가장 끝에 있는 부분을 끝마디 혹은 잎이라고 부릅니다. 마디는 노드라고도 합니다. 그리고 마디와 마디를 이어주는 선을 가지라고 부르고, 뿌리마디부터 가장 아래에 있는 끝마디까지 내려가기 위해 거쳐야 하는 가지의 수를 깊이라고 합니다. 위의 그림을 통해 조금 더 자세히 설명드리겠습니다.
맨 위에 하나의 뿌리마디가 있습니다. 뿌리마디는 데이터가 처음 갈라지기 시작하는 뿌리 역할로, 단 하나만 존재합니다. 이어서 뿌리마디가 다시 세 개의 중간마디(sunny, overcast, rain)로 갈라지는 것을 확인하실 수 있습니다. 이처럼 중간마디는 여러 개로 구성될 수 있습니다. 그리고 중간마디 중 sunny와 rain은 다시 한 번 갈라지고, overcast는 더이상 갈라지지 않고 그 자리에 멈췄습니다. 위의 그림에서 끝마디는 sunny에서 갈라진 2개, rain에서 갈라진 2개, overcaset로 총 5개입니다. 이처럼 더이상 분할이 이루어지지 않는 끝 부분을 모두 끝마디라고 부릅니다. 깊이는 뿌리마디부터 가장 아래에 있는 끝마디까지 가기 위해 거쳐야 하는 가지의 수이므로 2입니다.
의사결정나무를 구성하는 각 부분이 무엇인지에 대해서는 이제 알겠는데 어떻게 봐야하는 것인지는 잘 모르시겠다고요? 간단합니다! 뿌리마디부터 쭉 내려가면서 저와 함께 살펴봅시다.
우선 타겟변수(Dependent Variable)는 Play네요. 놀지(Play) 말지(Don't Play)를 분류하는 의사결정나무인 것으로 보입니다. 아직 분리가 일어나기 전인 뿌리마디를 살펴보면 전체 데이터가 14개(Play : 9, Don't Play : 5)로 이루어져 있는 것을 알 수 있습니다.
자, 이제 분리가 시작됩니다. 첫 번째 분리규칙은 Outlook입니다. 즉, 데이터의 독립변수 중 Outlook이라는 변수가 존재한다는 것이고, 그 Outlook 변수에 의해 세 개의 중간마디(sunny, overcast, rain)로 분리가 이루어진 것입니다. 분리된 세 개의 중간마디 중 rain을 같이 살펴볼까요? rain 마디는 5개(Play : 3, Don't Play : 2)의 데이터로 이루어져 있습니다. 아직은 분리가 덜 된 느낌이죠? Play와 Don't Play가 거의 반반에 가깝게 섞여있으니까요! 반면, overcast 마디는 4개(Play : 4, Don't Play : 0)으로 Play만으로 순수하게 구성되어 있습니다. 타겟변수가 얼마나 순수한 범주로 구성되어있느냐를 순수도라고 합니다. 이와 반대되는 단어는 불순도입니다.
rain을 이어서 살펴볼까요? rain의 순수도를 높이기 위해서는 분리를 더 해야할 것으로 보입니다. windy라는 변수에 의해서 rain에 있는 5개의 데이터가 다시 한 번 분리되었습니다. windy가 True이면 Don't Play이고, windy가 False이면 Play이네요! 이제 모든 끝마디가 굉장히 순수해졌습니다. 결과에 대한 해석은 뿌리에서부터 쭉 가지를 타고 내려가면서 차근차근 진행하시면 됩니다. 예를 들어 맨 오른쪽 아래에 있는 마디를 통해 결과를 해석해보면 다음과 같습니다.
"밖에 비가 오는 날(rain), 바람이 불지 않으면(windy False) 논다(Play)."
어떠신가요? 조금 정리가 되셨나요?😀
아래의 그림은 제가 임의로 만든 데이터 예시입니다. 아래의 데이터와 위의 의사결정나무 예시를 함께 살펴보시면 어떻게 분리가 수행된 것인지 조금 더 쉽게 이해하실 수 있으실겁니다! 데이터에 있는 독립변수들 중 하나(Outlook)를 골라서 첫 번째 분리규칙으로 사용했고, 분리 결과가 충분히 순수하지 못한 마디(sunny, rain)에 대해서는 다른 독립변수(humidity, windy)를 사용해서 2차적인 분리를 수행한 것입니다. 그런데 독립변수들을 어떤 순서로 선택해야 하는거냐고요? 걱정마세요! 그건 우리의 똑똑한 친구 의사결정나무가 알아서 해줄겁니다!😎 우리의 친구 의사결정나무가 각 분리 단계마다 어떠한 원리에 의해 독립변수를 선택하는지 한 번 살펴볼까요?

# 의사결정나무 분리 원리
의사결정나무는 모든 마디의 전체적인 불순도를 최대한 감소시키는 방향으로 분리를 수행합니다. 즉, 여러가지 독립변수들 중에 불순도를 가장 낮게 만들어줄 수 있는 독립변수를 선택하여 첫 번째 분리규칙으로 사용합니다. 그러기 위해서는 불순도를 측정할 수 있는 지수가 있어야겠죠? 일반적으로 범주형 타겟변수를 가지는 분류나무 모형에서는 지니지수, 엔트로피지수, 카이제곱 통계량의 p-value 등을 통해 불순도를 측정하고, 연속형 타겟변수를 가지는 회귀나무 모형에서는 분산 등을 통해 불순도를 측정합니다.
그중 가장 대표적으로 사용되는 것은 지니지수와 엔트로피지수입니다. 각각의 계산법과 간단한 예시를 살펴보겠습니다. 수식이 복잡하지 않으니 차근차근 보시면 금방 이해가 되실겁니다.
지니지수
지니지수부터 함께 살펴보겠습니다. 특정 마디 하나에 대한 지니지수는 아래와 같은 수식을 통해 계산할 수 있습니다. 여기서 c는 해당 마디를 구성하고 있는 타겟변수의 범주의 개수를 의미합니다. 그리고 pi는 해당 마디에서 i번째 범주가 차지하고 있는 비율을 의미합니다. 아래와 같은 수식을 통해 구한 끝마디들의 지니지수를 모두 합한 값이 최종 지니지수가 됩니다. 이해를 돕기위해 예시를 준비했습니다!
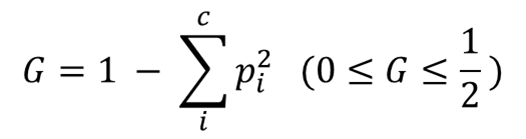

위와 같은 예시를 살펴봅시다. A와 B가 각각 6개로 구성된 어떤 데이터가 있습니다.
우선 분리가 이뤄지기 전의 지니지수를 계산해봅시다. A의 비율이 1/2이고, B의 비율이 1/2이므로 분리 전의 지니지수는 1/2가 됩니다. 간단하죠? 그런데 분리 후의 지니지수 계산 시에는 고려해야 하는 사항이 하나 더 있습니다. 바로 원래의 마디로부터 각 마디로 얼마만큼의 데이터가 할당되었느냐입니다.
위의 예시를 통해 설명드리겠습니다. 뿌리노드를 통해 원래 데이터가 총 12개라는 것을 알 수 있습니다. 그리고 12개의 데이터는 분리 후 왼쪽 마디에 8개, 오른쪽 마디에 4개가 할당되었습니다. 즉, 왼쪽 마디에는 전체의 2/3의 데이터가, 오른쪽 마디에는 전체의 1/3의 데이터가 할당된 것입니다. 이 값을 각각의 마디에 대한 지니지수 계산 후 곱해주어야 합니다. 위의 예시에 적혀있는 계산식처럼 말이죠!👍
결과적으로 분리 전에는 1/2였던 불순도가 1/8로 줄어들었음을 알 수 있습니다.
엔트로피지수
다음으로 엔트로피지수입니다. 특정 마디 하나에 대한 엔트로피지수는 아래와 같은 수식을 통해 계산할 수 있습니다. 여기서 c는 지니지수 때와 마찬가지로 해당 마디를 구성하고 있는 타겟변수의 범주의 개수를 의미합니다. 그리고 pi도 동일하게 해당 마디에서 i번째 범주가 차지하고 있는 비율을 의미합니다. 아래와 같은 수식을 통해 구한 끝마디들의 지니지수를 모두 합한 값이 최종 엔트로피지수가 됩니다. 이해를 돕기위해 예시를 준비했습니다!


log가 들어가서 다소 계산과정이 복잡해보일 수는 있으나 사실 지니지수와 크게 다르지 않습니다. 지니지수 때와 동일한 흐름으로 차근차근 계산해주시면 됩니다. 분리 후에는 지니지수 떄와 마찬가지로 전체 16개의 데이터가 각 마디에 8개씩 할당되었으므로, 1/2씩 곱해주게 됩니다.
결과적으로 분리 전에는 약 0.95였던 불순도가 약 0.75로 줄어들었음을 알 수 있습니다.
이처럼 의사결정나무는 어떤 지수를 사용하든 항상 불순도를 줄이는 방향으로 분리를 진행하며, 변수 하나하나를 비교해가며 가장 불순도를 많이 줄일 수 있는 변수를 분리규칙으로 선택하여 줄기를 뻗어 나아갑니다. 이 과정을 계속해서 반복하다보면 의사결정나무가 완성됩니다. 의사결정나무가 어떻게 탄생하는지 이제 이해가 되셨나요?
이번 포스팅에서는 가장 대표적인 분류 모형 중 하나인 의사결정나무에 대해 알아보았습니다. 제 글에 대해 추가로 궁금하신 점이나 지적해주실 부분이 있으시다면 언제든지 댓글 부탁드립니다!
'Data Analysis > Machine Learning' 카테고리의 다른 글
| Over-Sampling & Under-Sampling & SMOTE (0) | 2022.02.09 |
|---|---|
| 분류 vs 예측 (2) | 2022.02.09 |
| 지도학습 vs 비지도학습 (0) | 2022.02.08 |
| 인공지능 vs 머신러닝 vs 딥러닝 (0) | 2022.02.07 |