2021. 4. 18. 20:36ㆍData Analysis/Deep Learning

안녕하세요.
데이터 분석하는 새내기 대학원생, 석사 1학기 고니입니다.
지난 시간에는 딥러닝의 기본 개념인 인공신경망의 출발에 대한 이야기를 나누어보았습니다. 인공신경망은 사람의 신경망을 본떠 만든 네트워크 구조로, “기계가 사람처럼 생각하고 행동하는 것이 진정한 인공지능이 아닐까?”라는 생각에서 출발했습니다.
이번 시간에는 인공신경망의 초기 연구 단계에서 제안되었던 퍼셉트론에 대한 이야기를 나누어보려고 합니다. 퍼셉트론에 대해서 잘 이해하시고 나면 앞으로 공부하게 될 인공신경망과 딥러닝에 대한 이해가 굉장히 쉬워질 것입니다.
# TLU
지난 시간에 소개해드렸던 “인공신경망이라는 개념을 세상에 처음 등장시킨 두 인물”이 누구였는지 기억하시나요? 미국의 신경생리학자 워렌 맥컬록과 논리학자 윌터 피츠였습니다. 두 사람은 1943년, TLU라고 불리는 최초의 인경신경망을 제시했습니다. TLU는 오늘 함께 이야기를 나누어볼 퍼셉트론의 기초가 되는 모형이라고 생각하시면 됩니다.


TLU는 Threshold Logic Unit의 줄임말로, 아래 그림과 같이 굉장히 간단한 구조를 가지고 있습니다.

TLU는 이름에서부터 알 수 있듯이 Threshold(θ)를 기준으로 작동하는 모형입니다. 쉽게 말해 TLU는 계단 함수(Step Function)을 사용하여, Input의 합이 Threshold(θ)보다 크면 1을, 그렇지 않으면 0을 출력합니다. 이렇게 인공신경망에서 계단 함수처럼 입력된 값을 특정한 값으로 변환시켜주는 함수를 활성화 함수라고 부르는데 활성화 함수에 대한 자세한 이야기는 추후의 게시글에서 다루도록 하겠습니다.

만약 X1이 0.5이고 X2가 1이라고 가정했을 때, TLU의 Threshold(θ)를 1로 설정하면 X1+X2>Threshold(θ)가 성립하기 때문에 Output으로 1을 출력하게 됩니다.
반면, X1과 X2가 위와 동일할 때 TLU의 Threshold(θ)를 2로 설정하면, X1+X2>Threshold(θ)가 성립하지 않기 때문에 Output으로 0을 출력하게 됩니다. 정말 쉽지 않나요?
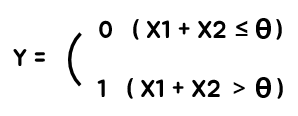
# 퍼셉트론
그리고 시간이 흘러 1957년, 미국의 심리학자 프랭크 로젠블래트가 TLU에 가중치라는 굉장히 중요한 개념을 추가하여 그 이름도 유명한 Perceptron(퍼셉트론)을 탄생시켰습니다.

"TLU에 가중치라는 개념을 추가한 것이 퍼셉트론이다."
퍼셉트론은 위의 한 문장으로 표현할 수 있습니다. 그러나 이렇게 말로만 설명해드리면 무슨 말인지 잘 감이 오지 않으실 것 같습니다. 앞서 살펴본 TLU와 마찬가지로 그림으로 살펴보면 이해하기가 훨씬 쉽습니다.

앞서 살펴본 TLU와 비슷해보이지 않나요? 보이시는 바와 같이 퍼셉트론은 TLU와 굉장히 비슷하지만 딱 한 가지 다른 점을 가지고 있습니다.
바로, 단순히 입력된 Input들이 그대로 더해지던 TLU와 달리 퍼셉트론에서는 각각의 Input들이 자신만의 고유한 가중치(Weight)와 곱해진 후 더해진다는 것입니다. 즉, TLU에서는 X1 + X2가 Threshold(θ)를 넘는지의 여부를 따졌다면, 퍼셉트론에서는 W1*X1 + W2*X2가 threshold를 넘는지를 따집니다.
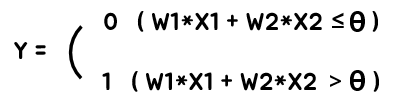
그렇다면 과연 가중치의 역할이 무엇이길래 TLU에는 없던 가중치가 퍼셉트론에는 새롭게 추가된 것일까요? 가중치는 각 입력값에 곱해짐으로써 각 입력값이 결과에 미치는 영향력을 조절하는 역할을 합니다.
X1의 가중치가 10, X2의 가중치가 1이라고 했을 때, X1의 변동이 X2의 변동보다 결과에 훨씬 큰 영향력을 미칠 것입니다. 이로 인해 각각의 입력 요소가 결과에 동일한 영향력을 행사하던 TLU와는 달리, 퍼셉트론에서는 중요한 입력 요소와 상대적으로 덜 중요한 입력 요소가 결과에 미치는 영향력을 서로 다르게 설정할 수 있게 되었습니다.
# 퍼셉트론의 논리 회로
퍼셉트론을 이용하면 아래 그림과 같이 다양한 논리 연산(AND, OR, NAND 등)이 가능합니다.

퍼셉트론이 어떻게 위와 같은 논리 연산을 수행할 수 있는지는 퍼셉트론의 연산방법을 살펴보면 쉽게 이해할 수 있습니다. 퍼셉트론은 앞서 소개해드린 바와 같이 아래의 연산을 수행합니다.

그리고 좌변이 우변보다 큰 경우에는 1을, 그렇지 않은 경우에는 0을 Output으로 출력하는 것이 퍼셉트론의 연산법입니다. 위 식에서 W1과 W2는 가중치로 상수이며, Threshold(θ)도 마찬가지로 상수입니다. 즉, 위의 식은 아래와 같이 정리할 수 있습니다.

이 때 W1, W2, Threshold(θ)가 상수라는 사실을 활용하면 위의 식은 Y = aX + b의 일차 함수꼴임을 알 수 있습니다.
(Y=X2, a=-W1, X=X1, b=Threshold(θ)/W2)

즉, 퍼셉트론은 선형 분류를 수행하는 분류기입니다. 다시 말해 퍼셉트론은 단 하나의 직선을 기준으로 분류를 진행할 수 있는 선형 분류기입니다. 물론 이 세상의 문제가 선형으로만 이루어져 있으면 정말 좋았겠지만, 야속하게도 세상은 그리 호락호락하지 않았습니다. 이 세상의 대부분의 데이터는 선형보다는 비선형의 형태를 띄고 있었습니다. 이에 로센블래트와 고등학교 동창이었던 미국의 과학자 마빈 민스키 박사는 XOR 논리 연산을 예시로 들며 퍼셉트론의 한계를 지적했습니다. 함께 살펴볼까요?

# 인공지능의 1차 겨울
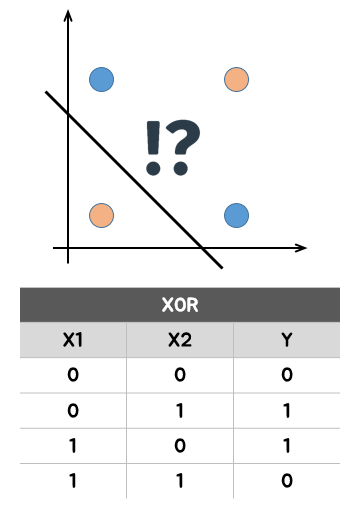
위의 그림은 퍼셉트론으로 XOR 논리 연산을 수행했을 때의 결과를 나타냅니다. 그런데 AND 연산과 OR 연산은 많이 들어봐서 익숙한데 XOR 연산은 무엇인지 잘 모르시겠다고요? (사실 제가 그랬습니다.)
XOR 연산은 X1과 X2가 서로 다를 때는 1을, 서로 같을 때는 0을 출력하는 연산 방법을 의미합니다.
과연 퍼셉트론은 XOR 연산을 정상적으로 수행할 수 있었을까요? 그림에서도 알 수 있듯이 선형 분류기인 퍼셉트론은 XOR 연산을 정상적으로 수행할 수 없었습니다.
퍼셉트론이 XOR 연산과 같은 비선형 문제를 해결할 수 없다는 한계가 밝혀지면서 인공지능은 1차 겨울을 맞이해야 했습니다. 활활 불타오르던 인공지능을 향한 연구는 순식간에 꺼져버렸고 점차 세간의 관심에서 멀어져만 갔습니다.
제 글에 대해 추가로 궁금하신 점이나 지적해주실 부분이 있으시다면 언제든지 댓글 부탁드립니다! 다음 시간에는 인공지능의 겨울을 깨고 부활의 신호탄을 쏘아올린 다층 퍼셉트론에 대해 다뤄보려고 합니다.
'Data Analysis > Deep Learning' 카테고리의 다른 글
| 대학원생이 알려주는 친절한 딥러닝 (5) - 활성화 함수 (4) | 2022.01.12 |
|---|---|
| 대학원생이 알려주는 친절한 딥러닝 (4) - 다층 퍼셉트론 (0) | 2021.05.11 |
| 대학원생이 알려주는 친절한 딥러닝 (2) - 인공신경망의 출발 (0) | 2021.04.09 |
| 대학원생이 알려주는 친절한 딥러닝 (1) - 딥러닝이란 (0) | 2021.04.08 |